| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| 30 |
- Face Alignment
- Markov transition matrix
- Facial Landmark Localization
- CIL
- learning to prompt for continual learning
- timm
- Class Incremental Learning
- Energy-based model
- state_dict()
- Continual Learning
- 베이지안 정리
- prompt learning
- PnP algorithm
- img2pose: Face Alignment and Detection via 6DoF
- Vector Quantized Diffusion Model for Text-to-Image Synthesis
- Face Pose Estimation
- mmcv
- DualPrompt
- CVPR2022
- Mask diffusion
- Class Incremental
- Mask-and-replace diffusion strategy
- VQ-VAE
- Discrete diffusion
- requires_grad
- Img2pose
- ENERGY-BASED MODELS FOR CONTINUAL LEARNING
- learning to prompt
- L2P
- VQ-diffusion
- Today
- Total
Computer Vision , AI
Deep learning 수학 기초 이론 [Bayes theorem편] 본문
글을 열면서
Deep learning 관련 논문을 보다 보면 자주 나오는 몇 가지 이론과 식들이 있는데 정리를 하지 않으니 한번 이해를 했어도 매번 까먹어서 다시 찾아보게 되는 상황이 와서 이번 기회에 차근차근 정리해보려 한다.
필요에 따라 구체적인 증명을 할 수도 있겠지만 수학적인 증명 같은 경우 잘 서술한 다른 글들이 많기 때문에
직관적인 이해와 어떤 때에 사용하는지에 대한 설명을 위주로 서술할 예정이다.
아마 지금 생각하고 있는 기준으로는 일단 Bayes theorem, Cross entropy, KL divergence, Monte Carlo method, Markov chain 정도 정리하지 않을까 싶다.
Bayes theorem
Bayes rule에 대한 간단한? 설명과 함께
Deep learning에서 Bayes theorem 사용하는 몇 가지 케이스에 대해서 짧게 적어본다.
Bayes theorem과 같은 경우
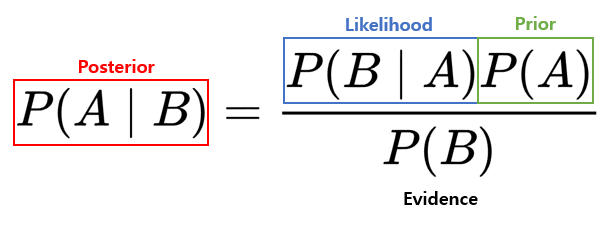
위와 같은 term으로 구성 되어 있고 고등학교 확률과 통계시간에 조건부 확률이라는 이름으로 보았을 것이다.
각 term이 의미하는 바는 다음과 같다.
Posterior: 우리가 '알고 싶은' 사후확률 (주로 우리가 관측하기 힘든 것)
Prior: 우리가 '알고 있는' 사전확률 (혹은 가정할 수 있거나)
Likelihood: A가 일어났다는 전제하에 B가 일어날 가능성 (주로 우리가 관측할 수 있는 것, P(A|B)에 대한 지지도)
Evidence와 같은 경우 이미 일어난 사건 B에 대한 확률로 prior와 likelihood로 표현가능하다. 본 포스팅에서 당장 설명하는데 크게 중요하지 않음으로 일단은 넘어가도록 한다.
핵심은 이렇다. 우리가 어떤 사건 B를 전제조건으로 갖는 사건 A 관측했다고 하자 이는 P(A|B)로 표현할 수 있다.
실제로 관측이 가능해서 바로 이 확률을 구할 수 있으면 제일 좋지만 경우에 따라 (사실 대부분의 경우에) 이 확률을 그냥 구할 수 없는 경우가 있다.
이런 경우 사건 A의 사전 확률 prior와 관측할 수 있는 likelihood를 바탕으로 우리가 알고 싶은 posterior 확률을 비교적 좀 더 정확하게 판단 해보겠다는 것이다.
예를 들면
사건 B가 터졌을 때 사건 A가 터질 확률을 알고 싶은 상황이다.
그런데 이에 대해 알 방법이 마땅치가 않은 상황이다.
그나마 다행인건 A에 대한 확률을 가정을 했던 어디선가 신뢰할만한 정보를 얻었던 미심쩍긴 해도 P(A)는 어디선가 얻어온 상황이고 운좋게도 P(B|A) 정도는 관측할만하다. 그렇다면 이를 바탕으로 추정을 하는거다
이렇게 설명하면 아무래도 잘 와닿지 않을 것이다.
결국에 우리가 P(A|B)를 알려면 P(B)야 비례식처럼 놓고 prior와 posterior의 관계를 구한다고 하더라도
P(B|A)도 알아야되고 P(A)도 가정을 하던 사전 정보가 주어졌던 알아야하는데
아니 그러면 도대체 P(A|B)가 관측이 불가능한데 P(B|A)는 관측이 가능한 그런 편의주의적인 상황이 있기는 한가? 있어도 이게 유용한가? 이런 생각이 들 수 있을 것이다.
여기에 대해 흔히 많이 드는 예시인 연어와 농어의 예시를 간략화하여 설명을 해보자
초짜 어부인 내가 바다에 나가서 낚시를 했다. 이 바다에서는 연어와 농어만 잡힌다고 가정을 해보자
이때 내가 물고기를 낚았는데 이게 연어인지 농어인지 어떻게 구분할것인가?라는 질문을 던질 수 있다.
우선 아는게 아무것도 없으니 이 바다에서 나는 연어(w1)와 농어(w2)의 비율은 0.5 대 0.5 반반이라고 가정하도록 하자
나는 초짜 어부라 잘은 모르지만 어디서 듣기로는 연어가 농어보다 피부색이 밝다고 한다. 그래서 우리는 피부색의 밝기(x)를 기준으로 연어와 농어의 분류를 진행할 것이다.
우리가 알고 싶은 Posterior 즉 피부색 밝기가 x일때 이게 연어(w1)인가? 는 P(w1|x)로 표기할 수 있다.
여기서 한가지 생각을 해보자 바다에서 피부색이 특정 값 x인 물고기들을 잡아서 연어인지 농어인지 분류하는게 쉽겠는가? 연어를 잡아서 연어의 피부색을 재는게 쉽겠는가 백이면 백 연어를 잡아서 연어의 피부색 통계 P(x|w1)를 내는게 쉽다고 할것이다. 그래서 우리는 비교적 만만한 방법을 선택하기 위해 연어를 열심히 잡아서 피부색에 대한 통계를 내던 도서관에 찾아가서 연어의 피부색 통계를 찾아보던 해서 연어의 피부색 분포 likelihood P(x|w1)을 구했다.
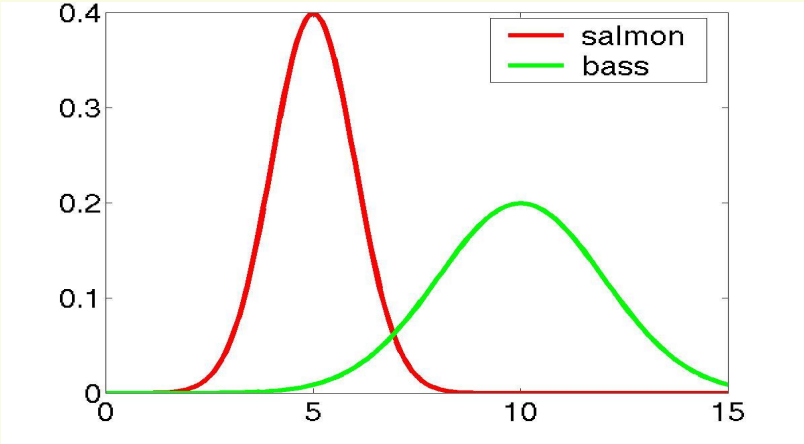
자 그러면 여기에 prior P(w1) 0.5를 곱하고 evidance로 나눠서 bayes rule 공식인 P(w1|x) = (P(x|w1)P(w1))/P(x)로 Posterior인 피부색이 x일때 연어일 가능성 P(w1|x)를 구할 수 있다!
마찬가지 방식을 농어에도 적용해 둘의 poseterior의 값을 비교해서 피부색이 x일 때 poseterior의 값이 높은 것을 선택하면 피부색으로 연어와 농어를 구분할 수 있는 판별법이 완성된다.
그런데 맙소사 생각보다 우리가 만든 연어 농어 판별법이 잘 들어 맞지 않는다는 소리를 듣고 다시 확인해보니 처음에 가정했던 연어와 농어의 비율 0.5대 0.5가 틀렸었다는 소식을 듣게 된다.
그래서 열심히 관련 통계를 찾아보니 아뿔싸 이 바다에서 잡히는 연어와 농어의 비율은 0.3대 0.7였던 것이다.
그래서 우리는 다급히 모델을 수정해 보기로 하고 점검에 들어간다. 지금 모델의 경우 Fig1을 기준으로 피부 밝기가 6쯤 되면 연어라고 판단을 하고 있다. 그런데 생각해보면 애초에 연어 자체가 30%의 확률로 잡히는데 피부 밝기가 6이라고 해서 연어라고 생각하는거 보단 피부가 좀 밝은 bass라고 생각하는게 훨씬 자연스럽다.
이를 반영하여 Prior P(w1)를 0.3로 수정하여 다시 모델을 개선을 한 결과 피부색이 어지간히 밝지 않고서야 연어일 Posterior 값 자체가 낮게 바뀌었다. 이전에 피부밝기가 6일때 연어라고 예측했던 모델이 농어라고 예측하게 된거다.
이런식으로 prior의 업데이트에 따라 bayes rule에 의한 예측 값은 바뀔 수 있고 likelihood만을 사용한 것에 비해 훨씬 합리적인 결과를 만들 수 있다.
서술이 상당히 길어졌는데 상기 예시처럼 P(A|B)를 알고싶은데 직접 구하기 어려운 경우 그래도 likelihood P(B|A)정도는 관측을 통해 얻을 수 있으면 prior P(A)를 통해서 likelihood를 조정해줌으로서 상당히 합리적인 판단을 할 수 있다.
요새는 발렌타인 데이에 초콜릿을 받았을 때 상대가 나를 좋아할 확률을 예시로 든다는데 기회가 되면 추가해보도록 하겠다.
맺으면서..
조건부 확률이라는 이름으로 많이 보았을 bayes rule의 경우 필자도 그러했지만 고등학교 교과 과정중에 거의 기계적으로 사용하기만 했을 것이다. 하지만 사실 bayes rule은 우리가 현실세계에서 실제로 구하기 힘든 어떤 조건부 확률 P(A|B)에 대해서 역확률인 P(B|A) 경우를 비교적 쉽게 관측할 수 있는 경우 P(B|A)로 P(A|B)를 나타낼 수 있는 굉장히 강력한 도구가 될 수 있다. 이 포스팅을 본 다른 분들도 이번 기회에 bayes rule을 사용해서 현실에서의 조건부 확률 예측을 한번 씩 해보는 것은 어떤가하는 생각이다.
# 현재 예시로 든 그림이 적절하지 못한 상황으로 (likelihood에 대한 graph만 있음 최종적으로 posterior에 대한 graph부재) 추후에 수정 및 추가 예정
'備忘錄' 카테고리의 다른 글
| timm 에러 cannot import name 'container_abcs' from 'torch._six' (0) | 2024.08.07 |
|---|---|
| MMCV 인식 불가 시 (0) | 2024.08.07 |
| [Torch] requires_grad 와 state_dict() 사이의 관계 (0) | 2024.08.06 |
| StyleGAN (1) | 2022.11.08 |

